Sáng kiến kinh nghiệm Giúp đối tượng học sinh trung bình, yếu nhận dạng và giải bài toán liên quan đến Giới hạn hàm số trong chương trình Toán Lớp 11

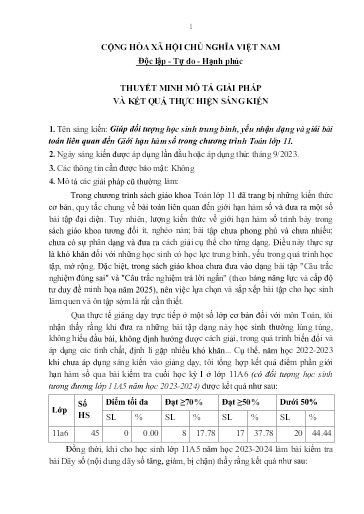
 2 
 Số Điểm 9, 10 Điểm 7, 8 Điểm 5, 6 Điểm dưới 5 
Lớp 
 HS SL % SL % SL % SL % 
11a5 42 0 0.00 5 11.91 14 33.33 23 54.76 
 Xuất phát từ thực tế đó, trong năm học 2023-2024 tôi đã tiến hành đổi mới 
phương pháp dạy học nội dung này tại lớp 11a5 (có chất lượng tương đương với 
lớp 11a6 trong khóa học trước), bằng cách vận dụng sáng kiến kinh nghiệm này. 
Trước khi thực hiện giải pháp, các phương pháp chủ yếu áp dụng trong dạy học 
các bài về giới hạn hàm số là: dạy học giải quyết vấn đề, kết hợp phương pháp dạy 
học nhóm và các phương pháp truyền thống....bám sát theo nội dung, chương trình 
sách giáo khoa hiện hành, trang bị kiến thức cơ bản cho học sinh sau đó vận dụng 
vào giải các bài tập trong sách giáo khoa. Tuy nhiên, để đáp ứng mục tiêu giáo 
dục với yêu cầu đổi mới phương pháp giảng dạy, các phương pháp trên còn một số 
hạn chế như: sự vận động của học sinh chưa toàn diện, sự trải nghiệm đồng thời về 
cùng một vấn đề nghiên cứu theo các kênh thông tin còn ít, sự phát triển đồng đều 
hài hòa phẩm chất và năng lực của học sinh đôi khi còn bị hạn chế. Đặc biệt đối 
với đối tượng học sinh trung bình và yếu thì khả năng tư duy phân tích, tổng hợp 
rất hạn chế, gần như giải bài nào biết bài đó. Việc tự phân loại bài toán, nhận dạng 
bài toán và hình thành phương pháp giải cho từng dạng, phương pháp giải chung 
là rất khó khăn. Hơn nữa, lượng thời gian dành cho tiết học trên lớp là không 
nhiều nên giáo viên giúp học sinh tổng hợp, phân dạng và đưa ra cách giải cụ thể 
là việc làm rất cần thiết. 
5. Sự cần thiết phải áp dụng giải pháp sáng kiến: 
 Toán học là một môn học đòi hỏi tư duy và logic, phải biết vận dụng và kết 
hợp nhiều kiến thức lại với nhau. Do đó, việc phân dạng và hình thành phương 
pháp giải từng dạng toán là biện pháp mang lại hiệu quả cao trong giảng dạy, đặc 
biệt với đối tượng học sinh có học lực trung bình, yếu. 
 Trong chương trình Toán lớp 11, việc phân loại và hình thành phương pháp 
giải các bài toán về giới hạn hàm số có vai trò rất quan trọng, nó có tính chất thực 
hành, tổng hợp và sáng tạo. Ngoài ra, nó củng cố, huy động nhiều kiến thức và rèn 
luyện được kỹ năng vận dụng kiến thức cơ bản. 
 Khi giải các bài tập về giới hạn hàm số, thầy và trò vừa phải nhớ kiến thức cơ 
bản, vừa phải xác định mối quan hệ của các dữ kiện từ đó hướng đến những điều 
cần tìm tòi. Do vậy, người học phải luôn tư duy, suy luận logic, cẩn thận, tỷ mỷ, 
 4 
sinh áp dụng, chú trọng các bài tập xuất hiện nhiều trong các đề kiểm tra định kỳ, 
đề thi tốt nghiệp THPT các năm, lược bỏ bớt một số bài, dạng phải tư duy sâu, 
mang tính hàn lâm, có sự liên hệ rộng để học sinh đỡ "sợ" môn Toán. Quy trình 
thực hiện là: Giáo viên phân loại dạng toán, đưa ra cách giải từng dạng một cách 
chi tiết và tường minh, giải bài tập mẫu, cho học sinh tự luyện tập các bài tập 
tương tự, giáo viên chữa, sửa sai và giao bài tập tương tự về nhà. Rèn luyện học 
sinh kỹ năng giải nhanh và giải bài tập trắc nghiệm. 
6. Mục đích của giải pháp sáng kiến: 
 Giải pháp góp phần nghiên cứu một cách có hệ thống, làm rõ hơn việc phân 
loại và đưa ra phương pháp giải bài toán về giới hạn hàm số trong chương trình 
Toán lớp 11. 
 Giúp học sinh nhận dạng và tìm ra phương pháp giải tối ưu, nhanh nhất một 
số dạng bài tập về giới hạn hàm số thường gặp trong các đề kiểm tra giữa học kỳ, 
cuối học kỳ, đề thi tốt nghiệp THPT và thi học sinh giỏi. Phát triển khả năng tổng 
hợp, khái quát hóa dạng toán và phương pháp giải chung. 
 Rèn luyện kỹ năng giải nhanh và giải bài tập trắc nghiệm. 
 Nâng cao trình độ chuyên môn, nghiệp vụ phục vụ cho công tác giảng dạy, 
ôn tập giữa học kỳ, cuối học kỳ, ôn thi học sinh giỏi và thi tốt nghiệp THPT. Đồng 
thời chia sẻ với đồng nghiệp những kinh nghiệm của bản thân. 
7. Nội dung: 
7.1. Thuyết minh giải pháp mới hoặc cải tiến 
7.1.1. Giải pháp 1: 
 - Tên giải pháp: Giúp học sinh phân loại, nhận dạng và đưa ra cách giải bài 
toán tối ưu nhất, vận dụng phương pháp vào thực hành giải bài toán. 
 - Nội dung: Lựa chọn dạng toán phù hợp đối tượng học sinh, phân loại các 
dạng toán, cách nhận dạng; đưa ra phương pháp giải cụ thể cho từng dạng toán, 
vận dụng giải một số ví dụ điển hình, bài toán mẫu. Chỉ ra những điểm cần chú ý, 
những sai lầm thường gặp và hạn chế của cách giải. 
 - Các bước tiến hành thực hiện giải pháp: 
Nghiên cứu lý luận: Nghiên cứu chương trình, sách giáo khoa, sách tham khảo và 
các đề thi, đề kiểm tra. 
Điều tra thực tiễn: Quan sát việc dạy và học phần kiến thức này qua các hình thức 
như dự giờ, trao đổi với đồng nghiệp, phỏng vấn trực tiếp 
 6 
Điều tra thực tiễn: Quan sát việc dạy và học phần kiến thức này qua các hình thức 
như dự giờ, sử dụng phiếu điều tra, phỏng vấn trực tiếp 
Tổng kết kinh nghiệm: Tổng kết kinh nghiệm của đồng nghiệp và bản thân trong 
quá trình dạy học. Đặc biệt là kinh nghiệm của những giáo viên có chuyên môn 
cao về vấn đề nghiên cứu của đề tài. 
Thực nghiệm sư phạm: Thực nghiệm sư phạm có đối chứng song song, tổ chức 
thực nghiệm ở lớp 11A5 và một số lớp cùng khóa có đối tượng học sinh tương 
đương điểm tổng kết năm lớp 10, một số lớp của một số trường trên địa bàn huyện 
Yên Thế, Tân Yên, so sánh kết quả học tập của học sinh ở khóa trước khi chưa áp 
dụng sáng kiến. 
Phương pháp thống kê: Sử dụng phương pháp thống kê toán học để phân tích kết 
quả. 
- Kết quả khi thực hiện giải pháp: Đã lựa chọn được hệ thống bài tập theo từng 
dạng toán phù hợp đối tượng học sinh, sắp xếp hệ thống bài tập theo dạng toán và 
phân loại các bài tập, sắp xếp từ dễ đến khó. 
+ Sản phẩm được tạo ra từ giải pháp: 
 (Chi tiết tại Phụ lục 2) 
+ Các bảng số liệu, biểu đồ so sánh kết quả trước và sau khi thực hiện giải pháp: 
Bảng 1: Tổng hợp điểm kiểm tra phần giới hạn hàm số ở lớp 11A6 năm học 
2022-2023 và lớp 11A4 năm học 2023-2024 (qua bài kiểm tra thường xuyên) khi 
chưa áp dụng sáng kiến kinh nghiệm. 
 Số Điểm tối đa Đạt ≥ 70% Đạt ≥ 50% Dưới 50% 
Lớp 
 HS SL % SL % SL % SL % 
11A6 
(2022- 45 0 0.00 8 17.78 17 37.78 20 44.44 
2023) 
11A4 
(2023- 39 0 0.00 9 23.08 14 35.90 16 41.02 
2024) 
 Qua Bảng 1, cho thấy khi chưa áp dụng sáng kiến điểm kiểm tra của học 
sinh phần giới hạn hàm số thấp (từ 41-45% dưới mức trung bình), tỷ lệ học sinh 
đạt điểm giỏi, khá cũng rất thấp (từ 18-23%). 
 8 
 Sáng kiến đã được tác giả áp dụng giảng dạy cho học sinh lớp 11A5 năm học 
2023-2024, Trường THPT Yên Thế. Đã được giới thiệu cho đồng nghiệp trong 
Trường THPT Yên Thế giảng dạy cho học sinh lớp 11A4, 11A6, 11A7. Đồng 
thời, giải pháp cũng được giới thiệu cho các đồng nghiệp trên địa bàn huyện Yên 
Thế, Tân Yên đưa vào giảng dạy cho học sinh như: Trường THPT Bố Hạ (lớp 
11A3), Trường THPT Mỏ Trạng (lớp 11A1), Trường THPT Tân Yên số 2 (lớp 
11A9), Trường THPT Nhã Nam (lớp 11A5). Bước đầu đã được các đồng nghiệp 
có những phản hồi và đánh giá tích cực (có văn bản xác nhận của các nhà trường 
đính kèm tại phụ lục 3). 
7.3. Thuyết minh về lợi ích kinh tế, xã hội của sáng kiến: 
 Sau khi áp dụng các giải pháp nêu trên ở tại các trường: THPT Yên Thế, 
THPT Bố Hạ, THPT Mỏ Trạng, THPT Tân Yên số 2, THPT Nhã Nam cho thấy 
hiệu quả của sáng kiến đạt được như sau: 
 Về lợi ích kinh tế 
 Những ưu điểm khi áp dụng sáng kiến vào giảng dạy môn Toán ở trường phổ 
thông: 
 - Tiết kiệm thời gian, công sức của giáo viên khi tổ chức dạy học, rèn kỹ 
năng cho học sinh. Giáo viên có thể sử dụng phần tóm tắt lí thuyết của sáng kiến 
để trau dồi kinh nghiệm và phát triển sâu, rộng thêm. Đồng thời, có thể vận dụng 
các giải pháp nghiên cứu của sáng kiến này để giải quyết các chủ đề tương tự khác 
cho môn Toán. Giảm đáng kể công sức, thời gian cho giáo viên trong việc tìm tòi, 
tổng hợp và phân dạng bài tập theo 3 dạng thức: "câu trắc nghiệm nhiều phương 
án lựa chọn", "câu trắc nghiệm đúng sai", "câu trắc nghiệm trả lời ngắn" cho học 
sinh ôn tập. 
 - Những giải pháp được nêu trong sáng kiến có thể trở thành tư liệu tham 
khảo cho giáo viên, tự nghiên cứu, xây dựng chủ đề dạy học hoặc làm tài liệu 
giảng dạy, rèn kỹ năng cho học sinh. 
 - Sáng kiến có thể sử dụng làm tài liệu tự học hữu hiệu cho học sinh. Tiết 
kiệm kinh phí mua tài liệu, sách tham khảo..., giảm thời gian học trên lớp. 
 Về lợi ích xã hội 
 - Khi Sáng kiến được áp dụng, bước đầu đã làm thay đổi nhận thức của học 
sinh khi học môn Toán, phát triển năng lực cũng như nâng cao kết quả học tập của 
học sinh. Sự chuyển biến tích cực đó bước đầu đã đóng góp một phần quan trọng 
giúp nâng cao kết quả học tập và rèn luyện của học sinh. Phát triển năng lực năng 
lực của học sinh trong học tập môn Toán cũng như với các môn học khác. 
 10 
 Phụ lục 1 
Sản phẩm được tạo ra từ giải pháp 1: Tóm tắt lý thuyết, phân loại dạng toán và 
đưa ra cách giải bài toán; vận dụng giải một số bài toán đại diện về giới hạn 
hàm số trong chương trình môn Toán lớp 11. 
I. KIẾN THỨC CƠ BẢN 
1) Giới hạn của hàm số tại một điểm 
a) Giới hạn hữu hạn 
Cho hàm số fx xác định trên khoảng ab; , có thể trừ điểm x0 a; b . Nếu với 
mọi dãy số xn mà xnn a; b \ x00 ; lim x x ta đều có lim f xn L thì ta nói hàm 
số fx có giới hạn là số L khi x dần đến x0 . Khi đó ta kí hiệu lim f x L hoặc 
 xx 0
f x L khi xx 0 . 
b) Giới hạn vô cực 
Tương tự như các điều đã nêu trong phần a, nếu L là thì ta nói fx có giới 
hạn vô cực khi xx 0 và kí hiệu lim fx hay fx khi xx 0 . 
 xx 0
2) Giới hạn của hàm số tại vô cực 
Cho hàm số fx xác định trong khoảng a; . Khi đó nếu với mọi dãy số xn 
với xnn a  n, lim x ta đều có lim f xn L (hoặc , ) ta nói hàm số fx 
có giới hạn là L (hoặc ) khi x dần tới vô cực. Khi đó viết lim L (hay ) 
 x 
hoặc f x L (hay ) 
Khi x hàm số fx trong ; b , với mọi dãy xn mà xnn blim x ta 
đều có lim f xn L (hay ) thì ta có lim f x L (hay ) hoặc f x L (hay 
 x 
 ) khi x 
Một số giới hạn của hàm số tại vô cực 
 11
* lim 0, lim 0 
 xx xx 
* lim xk (với ); lim xk nếu k chẵn và nếu k lẻ. 
 x x 
 11
* lim lim k * 
 xx xxkk 
3) Một số định lí về giới hạn hữu hạn 
Định lí: Nếu limf x L , lim g x M , c là hằng số thì 
 x x00 x x
 12 
Nếu A x , B x đều chứa nhân tử xx 0 ta sẽ tiếp tục phân tích thành các nhân tử. 
Chú ý: 
- Với f x , g x là đa thức (thường là hàm số bậc hai, bậc ba, bậc bốn) thì ta 
phân tích nhân tử bằng việc giải phương trình f x g x 0 
- Với f x , g x là căn thức, ta sẽ sử dụng phương pháp nhân liên hợp (liên hợp 
số hoặc liên hợp biến) để phân tích nhân tử. 
- Sử dụng các hằng đẳng thức, nhóm số hạng, phân tích ra thừa số bậc 2, chia đa 
thức, sơ đồ Hoócne, 
- Chia tách thành các phân thức bằng cách thêm bớt đại lượng đơn giản nhất theo x 
hoặc hằng số mà các giới hạn mới vẫn giữ nguyên dạng vô định 0 . 
 0
- Nếu limf x ; lim g x thì lim x g x ; lim x . g x 
 x x00 x x x x00 x x
3. Dạng 3: Dạng vô định 
 fx 
Bài toán : Tính lim khi limf x lim g x , trong đó f x , g x là các đa 
 x gx xx 
thức và căn thức. 
Phương pháp giải: 
Chia cả tử và mẫu cho xn với n là số mũ bậc cao nhất của biến số x trong mẫu 
thức. Nếu f x , g x có chứa biến x trong dấu căn thức thì đưa xk ra ngoài dấu 
căn (với k là số mũ bậc cao nhất của x trong dấu căn). 
Chú ý: 
* Khi x thì ta xử lý giống như với giới hạn của dãy số. 
* Khi x ta cần lưu ý khi đưa x2k ra ngoài dấu căn thức bậc chẵn. 
Dạng hay gặp chính là x2 x x khi x và x khi x 
 fx 
*Xét hàm số hx có hệ số của hạng tử bậc cao nhất của f x , g x lần 
 gx 
lượt là a, b 
Và kí hiệu degf x , deg g x lần lượt là bậc của f x , g x 
 fx 
- Nếu degf x deg g x thì lim 
 x gx